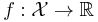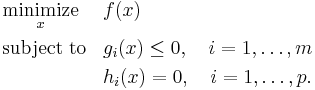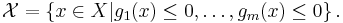Convex optimization
Convex minimization, a subfield of optimization, studies the problem of minimizing convex functions over convex sets. The convexity property can make optimization in some sense "easier" than the general case - for example, any local optimum must be a global optimum.
Given a real vector space  together with a convex, real-valued function
together with a convex, real-valued function
defined on a convex subset  of
of  , the problem is to find a point
, the problem is to find a point 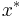 in
in 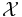 for which the number
for which the number  is smallest, i.e., a point
is smallest, i.e., a point 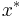 such that
such that
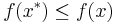 for all
for all 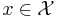 .
.
The convexity of  makes the powerful tools of convex analysis applicable: the Hahn–Banach theorem and the theory of subgradients lead to a particularly satisfying theory of necessary and sufficient conditions for optimality, a duality theory generalizing that for linear programming, and effective computational methods.
makes the powerful tools of convex analysis applicable: the Hahn–Banach theorem and the theory of subgradients lead to a particularly satisfying theory of necessary and sufficient conditions for optimality, a duality theory generalizing that for linear programming, and effective computational methods.
Convex minimization has applications in a wide range of disciplines, such as automatic control systems, estimation and signal processing, communications and networks, electronic circuit design, data analysis and modeling, statistics (optimal design), and finance. With recent improvements in computing and in optimization theory, convex minimization is nearly as straightforward as linear programming. Many optimization problems can be reformulated as convex minimization problems. For example, the problem of maximizing a concave function f can be re-formulated equivalently as a problem of minimizing the function -f, which is convex.
Contents |
Theory
The following statements are true about the convex minimization problem:
- if a local minimum exists, then it is a global minimum.
- the set of all (global) minima is convex.
- for each strictly convex function, if the function has a minimum, then the minimum is unique.
These results are used by the theory of convex minimization along with geometric notions from functional analysis such as the Hilbert projection theorem, the separating hyperplane theorem, and Farkas' lemma.
Standard form
Standard form is the usual and most intuitive form of describing a convex minimization problem. It consists of the following three parts:
- A convex function
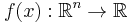 to be minimized over the variable
to be minimized over the variable 
- Inequality constraints of the form
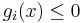 , where the functions
, where the functions 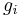 are convex
are convex - Equality constraints of the form
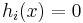 , where the functions
, where the functions 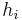 are affine. In practice, the terms "linear" and "affine" are often used interchangeably. Such constraints can be expressed in the form
are affine. In practice, the terms "linear" and "affine" are often used interchangeably. Such constraints can be expressed in the form 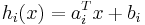 , where
, where 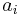 and
and 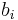 are column-vectors..
are column-vectors..
A convex minimization problem is thus written as
Note that every equality constraint  can be equivalently replaced by a pair of inequality constraints
can be equivalently replaced by a pair of inequality constraints 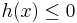 and
and 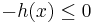 . Therefore, for theoretical purposes, equality constraints are redundant; however, it can be beneficial to treat them specially in practice.
. Therefore, for theoretical purposes, equality constraints are redundant; however, it can be beneficial to treat them specially in practice.
Following from this fact, it is easy to understand why 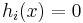 has to be affine as opposed to merely being convex. If
has to be affine as opposed to merely being convex. If 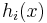 is convex,
is convex, 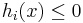 is convex, but
is convex, but 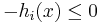 is concave. Therefore, the only way for
is concave. Therefore, the only way for 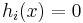 to be convex is for
to be convex is for 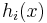 to be affine.
to be affine.
Examples
The following problems are all convex minimization problems, or can be transformed into convex minimizations problems via a change of variables:
- Least squares
- Linear programming
- Quadratic programming
- Conic optimization
- Geometric programming
- Second order cone programming
- Semidefinite programming
- Quadratically constrained quadratic programming
- Entropy maximization
Lagrange multipliers
Consider a convex minimization problem given in standard form by a cost function  and inequality constraints
and inequality constraints 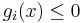 , where
, where 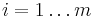 . Then the domain
. Then the domain  is:
is:
The Lagrangian function for the problem is
- L(x,λ0,...,λm) = λ0f(x) + λ1g1(x) + ... + λmgm(x).
For each point x in X that minimizes f over X, there exist real numbers λ0, ..., λm, called Lagrange multipliers, that satisfy these conditions simultaneously:
- x minimizes L(y, λ0, λ1, ..., λm) over all y in X,
- λ0 ≥ 0, λ1 ≥ 0, ..., λm ≥ 0, with at least one λk>0,
- λ1g1(x) = 0, ..., λmgm(x) = 0 (complementary slackness).
If there exists a "strictly feasible point", i.e., a point z satisfying
- g1(z) < 0,...,gm(z) < 0,
then the statement above can be upgraded to assert that λ0=1.
Conversely, if some x in X satisfies 1-3 for scalars λ0, ..., λm with λ0 = 1, then x is certain to minimize f over X.
Methods
Convex minimization problems can be solved by the following contemporary methods:[1]
- "Bundle methods" (Wolfe, Lemaréchal), and
- Subgradient projection methods (Polyak),
- Interior-point methods (Nemirovskii and Nesterov).
Other methods of interest:
Subgradient methods can be implemented simply and so are widely used.[2]
Maximizing convex functions
Besides convex minimization, the field of convex optimization also considers the far more difficult problem of maximizing convex functions:
- Consider the restriction of a convex function to a compact convex set: Then, on that set, the function attains its constrained maximum only on the boundary.[3] Such results, called "maximum principles", are useful in the theory of harmonic functions, potential theory, and partial differential equations.
Solving even close-to-convex problems can be computationally difficult. The problem of minimizing a quadratic multivariate polynomial on a cube is NP-hard.[4] In fact, in the quadratic minimization problem, if the matrix has only one negative eigenvalue, the problem is NP-hard.[5]
Extensions
Advanced treatments consider convex functions that can attain positive infinity, also; the indicator function of convex analysis is zero for every 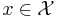 and positive infinity otherwise.
and positive infinity otherwise.
Extensions of convex functions include pseudo-convex and quasi-convex functions. Partial extensions of the theory of convex analysis and iterative methods for approximately solving non-convex minimization problems occur in the field of generalized convexity ("abstract convex analysis").
Software
Although most general-purpose nonlinear equation solvers such as LSSOL, LOQO, MINOS, and Lancelot work well, many software packages dealing exclusively with convex minimization problems are also available:
Convex programming languages
Convex minimization solvers
- MOSEK (commercial, stand-alone software and Matlab interface)
- solver.com (commercial)
- SeDuMi (GPLv2, Matlab package)
- SDPT3 (GPLv2, Matlab package)
- OBOE
- JOptimizer (Apache License v2.0, Java library)
See also
- Convex analysis
- Convex function
- Convex set
- Interior-point method
- Karush–Kuhn–Tucker conditions
- Lagrange multiplier
- Linear programming
- Optimization problem
- Optimization theory
- Pseudoconvex function
- Quadratic programming
- Quasiconvex function (with convex lower level sets)
- Semidefinite programming
- Subgradient method
References
- ^ For methods for convex minimization, see the volumes by Hiriart-Urruty and Lemaréchal (bundle) and the textbooks by Ruszczynski and Boyd and Vandenberghe (interior point).
- ^ Bertsekas
- ^ Theorem 32.1 in Rockafellar's Convex Analysis states this maximum principle for extended real-valued functions.
- ^ Sahni, S. "Computationally related problems," in SIAM Journal on Computing, 3, 262--279, 1974.
- ^ Quadratic programming with one negative eigenvalue is NP-hard, Panos M. Pardalos and Stephen A. Vavasis in Journal of Global Optimization, Volume 1, Number 1, 1991, pg.15-22.
- Bertsekas, Dimitri (2003). Convex Analysis and Optimization. Athena Scientific.
- Boyd, Stephen P.; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. ISBN 9780521833783. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved October 15, 2011.
- Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.
- Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
- Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). Convex analysis and minimization algorithms, Volume I: Fundamentals. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 305. Berlin: Springer-Verlag. pp. xviii+417. ISBN 3-540-56850-6.
- Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). Convex analysis and minimization algorithms, Volume II: Advanced theory and bundle methods. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 306. Berlin: Springer-Verlag. pp. xviii+346. ISBN 3-540-56852-2.
- Kiwiel, Krzysztof C. (1985). Methods of Descent for Nondifferentiable Optimization. Lecture Notes in Mathematics. New York: Springer-Verlag. ISBN 9783540156420, ISBN 3540156429.
- Lemaréchal, Claude (2001). "Lagrangian relaxation". In Michael Jünger and Denis Naddef. Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. 2241. Berlin: Springer-Verlag. pp. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR1900016.
- Nesterov, Y. and Nemirovsky, A. (1994). 'Interior Point Polynomial Methods in Convex Programming. SIAM
- Nesterov, Yurii. (2004). Introductory Lectures on Convex Optimization, Kluwer Academic Publishers
- Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
- Ruszczyński, Andrzej (2006). Nonlinear Optimization. Princeton University Press.
External links
- Stephen Boyd and Lieven Vandenberghe, Convex optimization (book in pdf)
- EE364a: Convex Optimization I and EE364b: Convex Optimization II, Stanford course homepages
- 6.253: Convex Analysis and Optimization, an MIT OCW course homepage
- Haitham Hindi, A tutorial on convex optimization Written for engineers, this overview states (without proofs) many important results and has illustrations. It may merit consultation before turning to Boyd and Vandenberghe's detailed but accessible textbook.
- Haitham Hindi, A Tutorial on convex optimization II: Duality and interior-point methods
- Brian Borchers, An overview of software for convex optimization
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||